几何画板正方形与正三角形迭代规律课件

迭代法是常用的一种数学方法，就是将一种规则反复作用在某个对象上，它可以产生非常复杂的行为。我们这里以利用几何画板探讨正方形与正三角形迭代镶嵌规律为例介绍图形迭代的方法。

几何画板制作探讨正方形与正三角形迭代镶嵌规律课件样图：

几何画板课件模板——探讨正方形与正三角形迭代镶嵌规律

什么是图形迭代？

给定初始图形F0，以及一个替换规则R，将R反复作用在初始图形F0上，产生一个图形序列： R（F0）＝F1，R（F1）＝F2，R（F2）＝F3，。。。

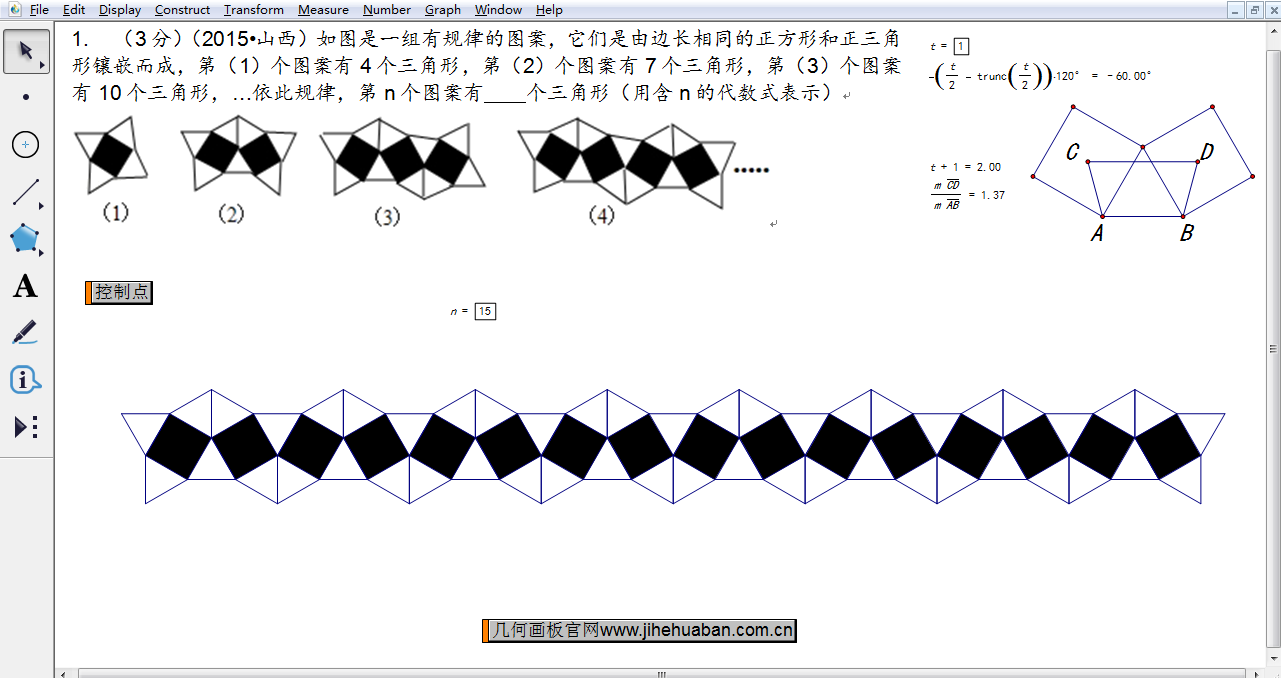
对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的。在该课件中，我们可以任意改变参数n的值，观察第n个图案是由多少个正方形和正三角形，从而得出一个规律。

在正多边形中，只有三种能用来铺满一个平面而中间没有空隙，这就是正三角形、正方形、正六边形。因为正三角形的每一个角等于60度，六个正三角形拼在一起时，在公共顶点上的六个角之和等于360度；正方形的每个角等于90度，所以四个正方形拼在一起时，在公共顶点上四个角的和也刚好等于360度；正六边形的每个角等于120度，三个正六边形拼在一起时，在公共顶点上的三个角之和也等于360度，如果用别的正多边形，就不能达到这个要求。

《图形中的规律》是北师大版小学数学第八册《认识方程》这单元的后续学习内容的第一课时，探索规律是《数学课程标准》实验教材新增的内容，也是教材改革的新变化之一。它蕴涵着深刻的数学思想，对学生进行思维训练，是学生今后学习、生活最基础的知识之一。

点击下面的“下载模板”按钮，即可下载该课件，用于研究正方形与正三角形迭代镶嵌规律。其实谢尔宾斯基三角形算是比较简单的分形图形，很有规律。我们也可以利用几何画板迭代功能画出谢尔宾斯基三角形，具体教程可参考谢尔宾斯基三角形的制作。