几何画板演示二次函数切线

二次函数是中学阶段接触最多的一种函数了，也是我们最开始学习解析几何的起点，二次函数的图象我们很熟悉，除此之外，我们还会研究的它的切线问题。下面就来介绍几何画板二次函数切线的演示过程。

几何画板演示二次函数切线课件样图：

几何画板演示《二次函数切线》课件示例

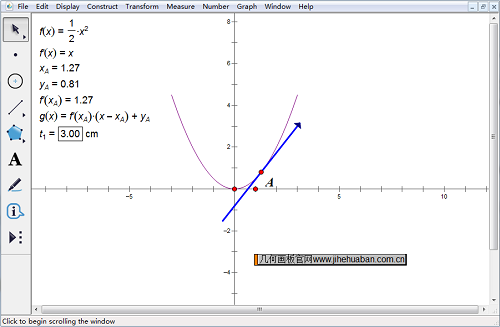
二欠函数是一条平滑的曲线，这种平滑的曲线也会涉及到切线问题。切线与函数相切，因此只能有一个交点。在这个课件中，点A就是抛物线上的一点，经过这一点作抛物线的切线，刚直线与抛物线就只有A点这一个交点，此时经过A点的这条直线就是抛物线的切线。用鼠标点住A点，就可以将A点在抛物线上进行任意的移动，在移动的同时，相应的切线也是随之变化，在这个变化的过程中，我们可以看到切线是在不断变化的，直线的斜率也在来断地发生变化，所以抛物线上的任意一点都会有切线，这些切线的斜率都不相同。当把A点移动到抛物线的顶点处时，会发现这时的切线是一条水平直线，与x重合，如果顶点不是原点，刚切线将会是一条与x轴平行的直线。

二次函数的切线很好理解，在计算相关的交点时，可以将一次函数与二次函数的表达式结合起来，再利用其它的已知条件就可以进行计算了。

点击下方的“下载模板”就可以将课件下载下来进行演示了。几何画板二次函数切线是一个比较好理解的概念，尤其是学习过了圆的切线以后，对切线的概念已经有了一个既成的概念，在此基础上，再加以函数的计算就可以很好的理解了。几何画板函数演示可以将数形结合起来，让学生从整体来理解数学问题，这其中几何画板动画功能发挥了很大的作用。如果想要了解更多几何画板函数课件的演示，可以参考课件：几何画板演示对数函数的动态图象。