利用几何画板构造三维曲面

对于初学画板的版友来说，用《几何画板》绘制三维函数曲面有一定的困难，制作这样的课件难免会效率低。针对这样的情况，小编这里给大家介绍一个使用几何画板多年的版友制作的三维曲面课件，本课件给出了一个在几何画板中绘制各种三维函数曲面的通用方法，下面就做详细介绍。

利用几何画板构造的三维曲面课件样图：

几何画板课件模板——构造的三维曲面示例

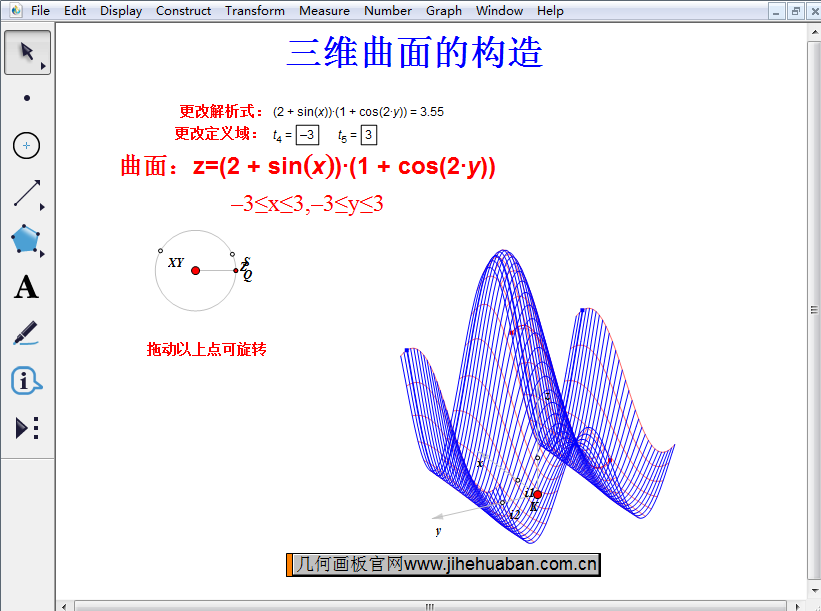
在该课件中，拖动圆上的点Q，就可以改变圆的半径，从而放大曲面，便于更详细的观察；移动圆上的点XY和点Z，可以将三维曲面进行旋转，更详细地观看到每面的特征。更灵活的是，可以自由修改函数解析式，观看自己所需函数的三维曲面效果，而且可以更改函数定义域，操作起来非常灵活。

什么是二次曲面？

二次曲面是在三维坐标系（x、y、z）下三元二次代数方程对应的所有图形的统称。最常见的二次曲面是球面和直圆柱面及直圆锥面。此外，二次曲面还包括椭球面、双曲面（又分为单叶双曲面和双叶双曲面）和抛物面（又分为椭圆抛物面和双曲抛物面，后者又称马鞍面）。

椭球面在3个对称轴上截得的线段，称为它的轴。当三个轴长相等时即为球面。当两个轴长相等时，它是由平面上的椭圆绕其对称轴旋转而成的旋转椭球面，一般椭球面实际是一个压扁了的旋转椭球面，它是二次曲面中仅有的一类限制在有限范围内的封闭曲面。平面上的双曲线分别绕它的虚轴和实轴旋转，得到旋转单叶双曲面和旋转双叶双曲面。平面上的抛物线绕它的对称轴旋转得到旋转抛物面。

该课件方法原理易懂，步骤简单，方便学习，能从不同角度观察图像，且作简单的改变便可以得到其他函数的图像，有助于提高学习效率和教学效果。点击下面的“下载课件”模板即可下载该课件，用于研究三维函数曲面的教学中。更多关于几何画板制作的三维曲面课件模板，可参考：几何画板动态演示曲面旋转变换效果。