如何用几何画板验证完全平方公式

完全平方公式是进行代数运算与变形的重要的知识基础。为了方便学生们完全学透该知识，教科书上给出了两种方法进行了证明：一运用了多项式乘以多项式，二是用几何图形进行了解释。对于完全平方公式的几何证明可以借助专业的绘图工具几何画板来完成，下面就一起学习用几何画板验证完全平方公式的方法。

具体的制作步骤如下：

步骤一 新建参数a、b。打开几何画板，执行“数据”——“新建参数”命令，在弹出的对话框输入参数名称a，数值为6，单位选择距离。按照这样的方法新建参数b=2.00cm，并执行“数据”——“计算”命令计算出a+b的值，如下图所示。

在几何画板中新建参数a、b示例

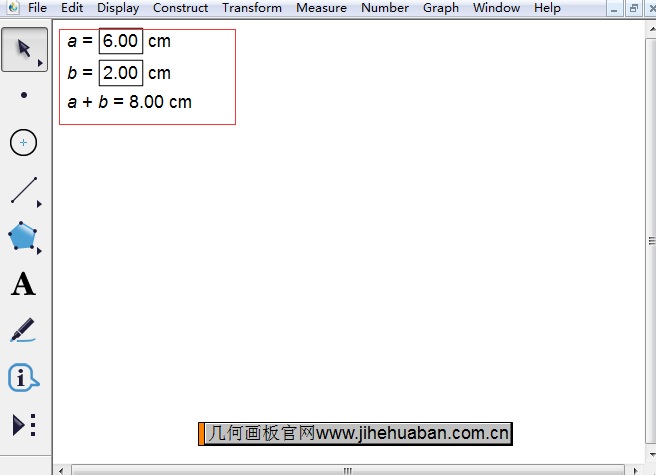
步骤二 以a+b的值为边长构造正方形。用移动工具选中计算数值，执行“变换”——“标记距离”命令。使用点工具在画板上任意画一点A，选中点执行“变换”——“平移”命令，在弹出的对话框修改角度为0，点击确定，即可得到点B。构造线段AB，双击点A标记为旋转中心，选中线段AB执行“变换”——“旋转”命令，角度为90，点击确定，即可得到点D。选中点D和线段AB构造平行线，同样选中点B和线段AD构造平行线，交点为C，构造线段BC、CD，得到正方形ABCD。

在几何画板中构造正方形ABCD示例

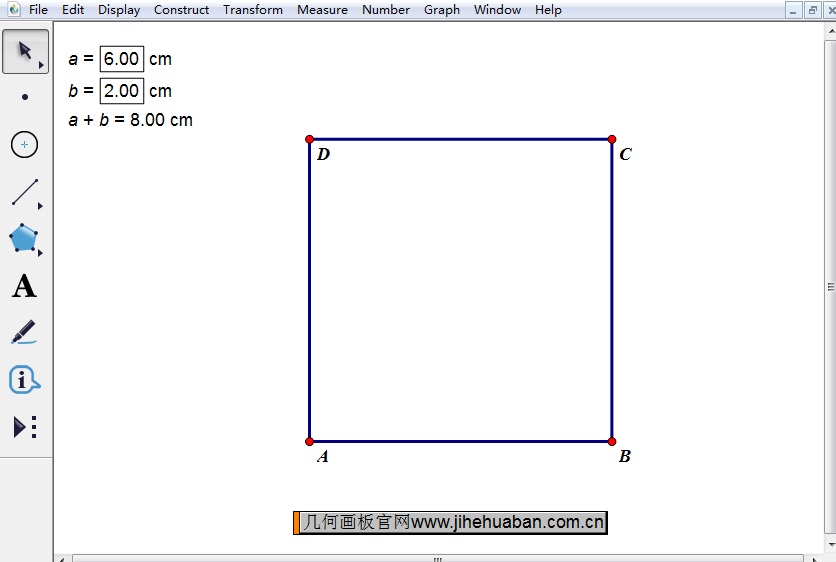
步骤三 划分正方形。选中参数a执行“变换”——“标记距离”命令，选中点A执行“变换”——“平移”命令，在弹出的对话框角度为90，点击确定，得到点A’。 选中参数b执行“变换”——“标记距离”命令，选中点C执行“变换”——“平移”命令，在弹出的对话框角度为180，点击确定，得到点C’。过点A’构造AB边的平行线，过点C’构造边AD的平行线，得到交点E。隐藏平行线，构造如下图所示的线段。

将正方形ABCD划分为四个四边形示例

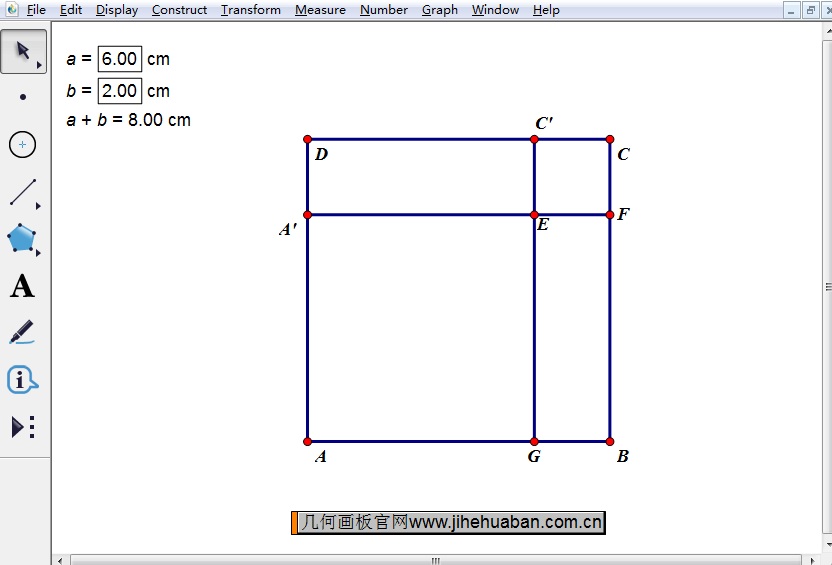
步骤四 计算将正方形ABCD的面积和分割的四个四边形的面积。正方形ABCD的面积可以表示为：（a+b）*（a+b），并通过计算得知其值。通过计算可以得出四个小的四边形的面积分别为：ab、ab、a²、b²，通过计算将四个小四边形的面积相加，得到的值应该和正方形ABCD的面积相等，从而可以验证完全平方公式的正确性。

计算数值验证完全平方公式示例

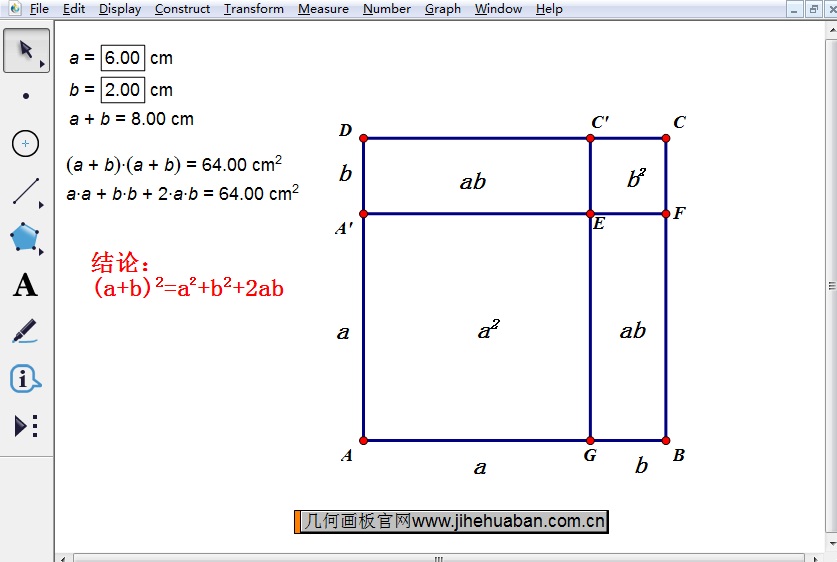
完全平方公式这一教学内容是学生在已经掌握单项式乘法、多项式乘法及平方差公式基础上的拓展，为了让学生们更加深刻地理解该公式，可以利用以上方法进行验证。几何画板还可以用来验证海伦公式，具体可参考：利用几何画板验证海伦公式。