利用几何画板演示探求最短距离

利用轴对称的性质，可以解决生活中很多“距离最短”问题，比如我们熟悉的“将军饮马”问题、“造桥”问题等等，平时讲课中老师需要很多复杂的画图、解释，操作起来耗时耗力，结果学生听得一知半解，每次遇到类似题目又不知道如何去解题了。所以这时如果能利用几何画板度量线段长度、移动点的位置感受图形及距离的变化，从而在实际操作中让学生去学习并得出结论，下面就以建造水泵站为例，一起学习用几何画板制作探求最短距离课件的方法。

几何画板制作的探求最短距离课件样图：

几何画板课件模板——演示探求最短距离课件示例

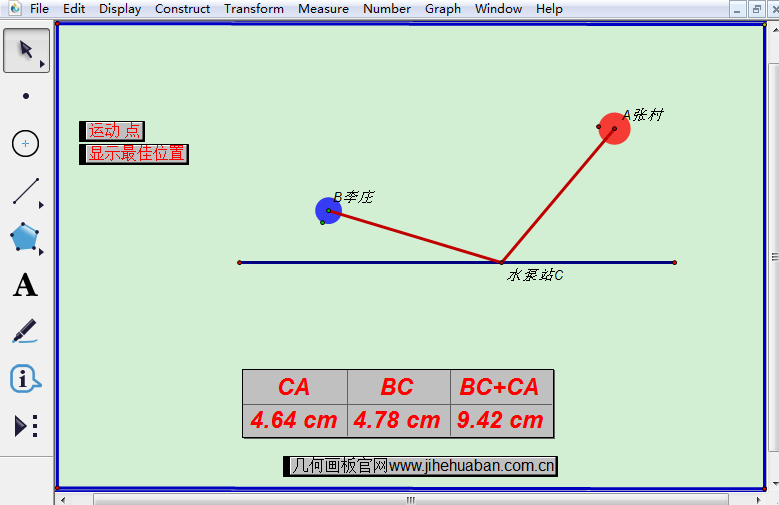
在该课件中，要在直线c上建造一个水泵站，以供张村和李庄人的使用，点击“运动点”动画按钮，就可以动态演示表示水泵站的点C在直线上左右运动，运动的同时，下方度量的线段CA、BC的长度和两线段和都在不断变化，可以一目了然的看到建造水泵站要使用的管子的长度。

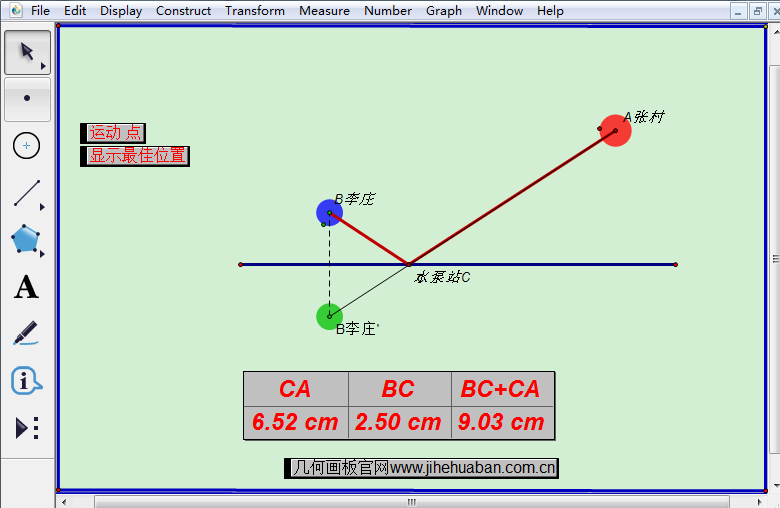
点击“显示最佳位置”操作按钮，就会自动作出点B关于直线对称的点B’，可以想象一下把李庄搬到这里来，然后连接点AB’，通过两点之间直线最短的定理，得到与直线的交点，即为建造水泵站的最佳位置。当点C运动到此交点处，可以知道总长度为9.03cm。

探求的最短距离示例

点击下面的“下载模板”按钮，即可下载该课件，用来给学生们讲解利用轴对称解决最短距离的问题，这类问题是考试必考内容，所以掌握很有必要。在解决动点问题中，仅借助黑板很难达到动的效果，部分学生对这种问题缺乏感性认识，想象不出运动形成怎样的图形，觉得很抽象，所以学得很吃力。借助几何画板，把动态问题转化到图形的运动中，让学生直观感受到图形的变化，问题就容易解决了。利用几何画板还可以探究圆上的点到定直线的距离最值，具体可参考：探究圆上的点到定直线的距离最值。