利用几何画板验证托勒密定理

托勒密定理也是几何学中的重要定理之一，是指圆内接四边形两组对边乘积的和等于其两条对角线的乘积。托勒密定理在解决初中平面几何及代数的某些问题时有它独到之处，为了让学生们更好地认识并理解该定理，可以用几何画板作图，通过多次实验来验证该定理的正确性，从而让学生们掌握该定理。

几何画板制作的验证托勒密定理课件样图：

几何画板课件模板——验证托勒密定理课件示例

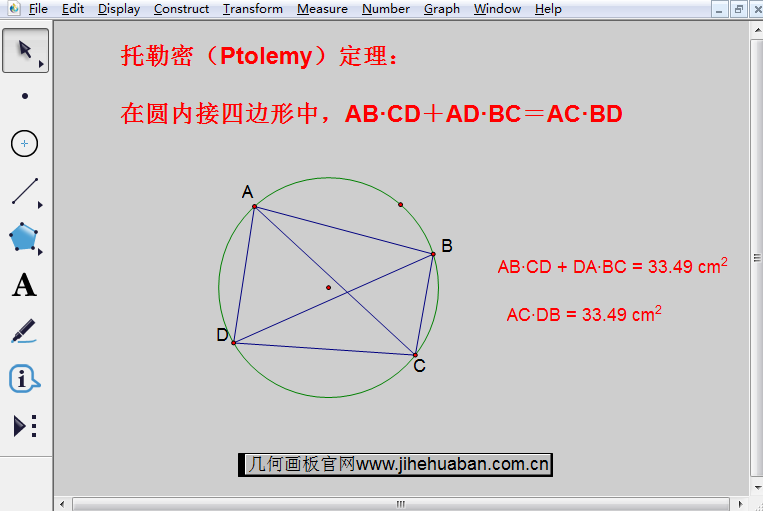
在该课件中，为了验证该定理，可以使用“移动工具”选中四边形的四个顶点，改变圆内接四边形的形状，与此同时，你会发现，不管四边形的形状怎么改变，在右边计算的四边形的对边乘积的和始终等于对角线乘积，从而可以验证该定理是恒成立的。

通过演示该课件，可以获知：

1.任意凸四边形ABCD，必有AC•BD≤AB•CD+AD•BC，当且仅当ABCD四点共圆时取等号。

2.托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆。

托勒密不等式：凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当共圆或共线。

简单的证明：复数恒等式：(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d)，两边取模，得不等式AC•BD≤|(a-b)(c-d)|+|(b-c)(a-d)|=AB•CD+BC•AD。

从托勒密定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质。

点击下面的“下载模板”按钮，即可下载该课件，用来在课堂上给学生们验证托勒密定理，从而加深学生们的理解，更好地运用该定理解几何题目。几何学中的大部分定理都是可以用几何画板进行验证的，比如海伦公式，大家如果不清楚怎么去用几何画板验证，可参考：利用几何画板验证海伦公式。