发布时间:2016-06-22 10: 40: 16
在学习勾股定理的相关知识时,课本上有提到用赵爽弦图来验证该定理,在黑板上无法对图形进行动态演示,无法让学生们真正地理解。现在几何画板这一款动态课件制作工具的出现,弥补了黑板式教学的不足,下面我们就一起来看看用几何画板制作赵爽弦图证明勾股定理课件的方法。
中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。
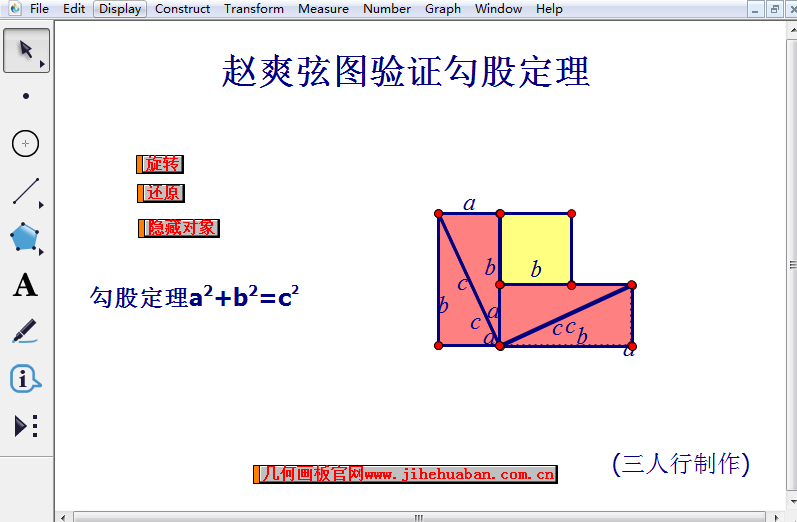
在该课件中,点击“旋转”操作按钮,就可以演示将两个直角三角形进行旋转,拼成一个大的正方形,如下图所示。
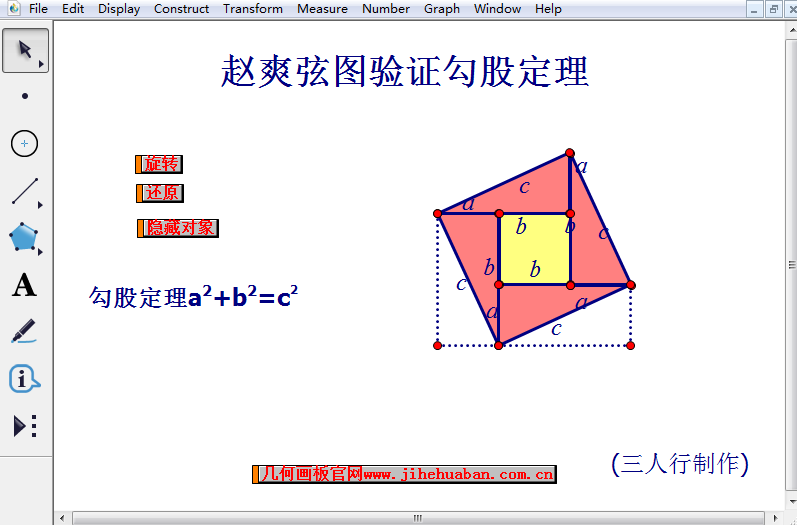
点击“还原”操作按钮,就可以将该课件还原到初始状态。如果不知道该课件是如何制作的,点击“隐藏对象”操作按钮,就可以显示出制作该课件的度量数据,方便了解该课件的制作技巧。
以弦为边长得到的正方形是由4个相等的直角三角形再加上中间的那个小正方形组成的。每个直角三角形的面积为ab/2;中间的小正方形边长为b-a,则面积为(b-a)2。
赵爽的这个证明可谓别具匠心,极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。
点击下面的“下载模板”按钮,就可以免费下载该课件,用于勾股定理的教学中。前面的教程中给大家介绍了用几何画板演示采用等积法验证勾股定理,如有疑问,可参考:几何画板验证勾股定理。
展开阅读全文
︾