利用几何画板动态演示九点圆

九点圆是几何学史上的一个著名问题，是指三角形三边的中点，三高的垂足和三个欧拉点（连结三角形各顶点与垂心所得三线段的中点）九点共圆。前面教程给大家介绍了用几何画板画九点圆的方法，其实还可以借助几何画板给学生们演示不同情况下的九点圆，本节就一起来学学用几何画板动态演示九点圆的方法。

几何画板演示三角形的九点圆课件样图：

几何画板课件模板——动态演示三角形的九点圆

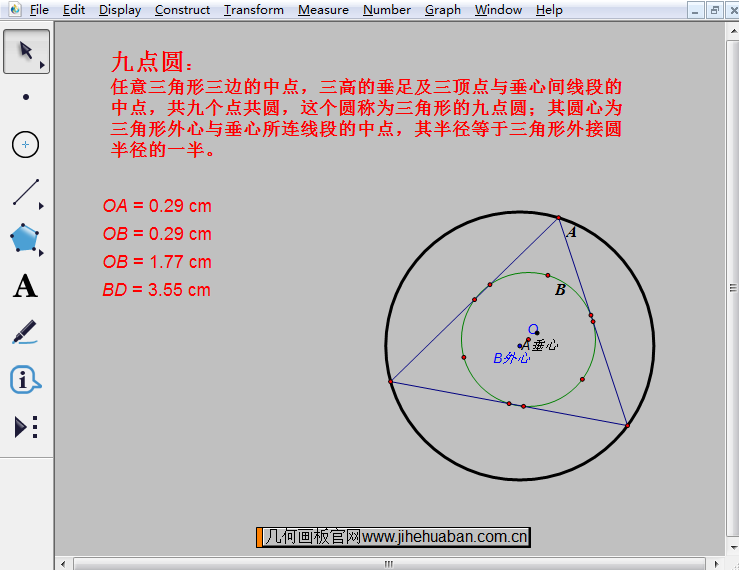
在该课件中，通过左边测量的线段可以知道圆心与各个点之间的距离，想要观察不同情况三角形的九点圆，可以任意选中三角形的三个顶点，然后在大圆上进行拖动，改变三角形的形状，从而观看不同情况下，三角形的九点圆，从而发现有什么异同。

九点圆具有许多有趣的性质，例如：

1.三角形的九点圆的半径是三角形的外接圆半径之半；

2.九点圆的圆心在欧拉线上，且恰为垂心与外心连线的中点；

3.三角形的九点圆与三角形的内切圆，三个旁切圆均相切（费尔巴哈定理）；

4.九点圆是一个垂心组（即一个三角形三个顶点和它的垂心，共四个点，每个点都是其它三点组成的三角形的垂心，共4个三角形）共有的九点圆，所以九点圆共与四个内切圆、十二个旁切圆相切。

5.九点圆心（V），重心（G），垂心（H），外心（O）四点共线，且HG=2OG，OG=2VG，OH=2OV。

九点圆圆心的重心坐标的计算跟垂心、外心一样麻烦。

设d1，d2，d3分别是三角形三个顶点连向另外两个顶点向量的点乘，并令c1=d2d3，c2=d1d3，c3=d1d2；c=c1+c2+c3。

那么重心坐标为：( (2c1+c2+c3)/4c，(2c2+c1+c3)/4c，(2c3+c1+c2)/4c )。

点击下面的“下载模板”按钮，即可下载该课件，用来给学生们动态演示三角形的九点圆，如果你对用几何画板画九点圆的方法还有疑问，可参考教程：如何用几何画板画九点圆。