探究三角形内接长方形面积最值问题

初中几何讲到三角形内接长方形最值问题，例如如何在三角形材料上剪裁出面积最大的长方形。这个问题要综合运用代数，几何知识，理解运用相似三角形的性质和二次函数的性质解决是该题的重难点，本课件案例试图渗透数形结合的思想与方法，用几何画板动态演示最值问题，将代数和几何图形巧妙结合，突破理解难点。

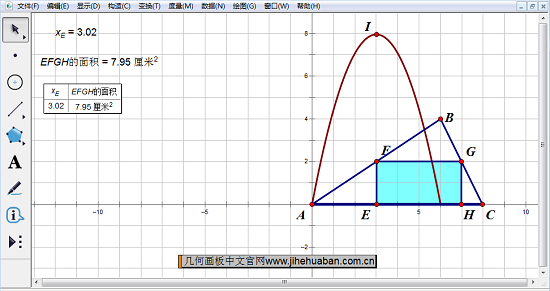
在几何画板中演示三角形内接长方形面积最值问题

课件制作的基本过程如下：

建立坐标系，隐藏单位点，以原点A、第一象限内点B，x轴正半轴上一点C构造三角形ABC。

构造线段AC上一点D、线段AD及其线段上的点E，过E作AC的垂线交AB于F，过F作EF的垂线交BC于G，过G作FG的垂线交AC于H。顺次选中EFGH，构造四边形内部，点击右键选中父对象，构造线段，隐藏垂线。

依次度量点E的横坐标x_E和长方形EFGH的面积，依次选中点x_E的横纵坐标和EFGH的面积绘制点I，选中E和I绘制I的轨迹。用鼠标拖动E到D点处，将D隐藏。此时拖动D点，即可引起轨迹的变化。

将x_E和EFGH的面积值制表，拖动E点，当I处于轨迹的最高处时，EFGH的面积为最大值。

从该课件可以看出，在寻求三角形内接长方形最大面积中，点E可以在三角形AC边上移动，移动点E来控制长方形长与宽，进而影响长方形的面积。在移动点E的过程，表中显示点E的横坐标的变化和对应内接长方形的面积的变化，从表格长方形面积随点E横坐标的变化而变化的动态数据中，可以观察点长方形面积最大时点E的坐标，这是通过数据的动态变化，观察最值问题。当然，随着点E的 移动，长方形的面积不仅以数据显示，它的面积在图上以轨迹显示，该轨迹是开口向下的二次函数图像，从中形象观察出面积最大，就是该轨迹到达二次函数的顶点位置。

该课件结合了图表的数据和图形的动态变化，数形结合动态演示了三角形内接长方形的最值问题。突破了学生难以理解的重难点，实现了数形结合的数学思想方法的渗透。点击下面的“下载模板”，可下载该课件模板，动态演示操作。最全的几何画板课件下载，尽在几何画板网站，欢迎访问。